Post 1, Aesthetic Exploration: Non-Euclidean Geometry in Art: A Gateway to Otherworldly Visuals

Imagine stepping into a world where lines curve endlessly, patterns repeat in mesmerizing ways, and the very fabric of space seems to shift and bend before your eyes. This is the essence of the non-Euclidean geometry art aesthetic, a style that incorporates the principles of curved and distorted spaces to create visuals that challenge our perception of reality.

To understand this captivating approach, it helps to start with the familiar: Euclidean geometry, also known as classical geometry, which many of us learned in high school. Named after the ancient Greek mathematician Euclid, this system of geometry defines the rules we instinctively recognize in everyday life: straight lines, flat planes, and angles that behave predictably. It forms the backbone of classical perspective in art, where lines converge neatly on the horizon to create depth and order.

But what happens when those straight lines start to bend, and planes curve like the surface of a sphere? Non-Euclidean geometry challenges the usual rules, giving rise to spaces that twist, converge, and expand in ways that defy intuition. Artists inspired by these ideas create distorted, curving, and often psychedelic visuals that mimic the behavior of lines on curved surfaces, such as spheres or hyperbolic planes. These works are not only mathematically intriguing but also visually striking, immersing viewers in patterns that seem infinite and otherworldly.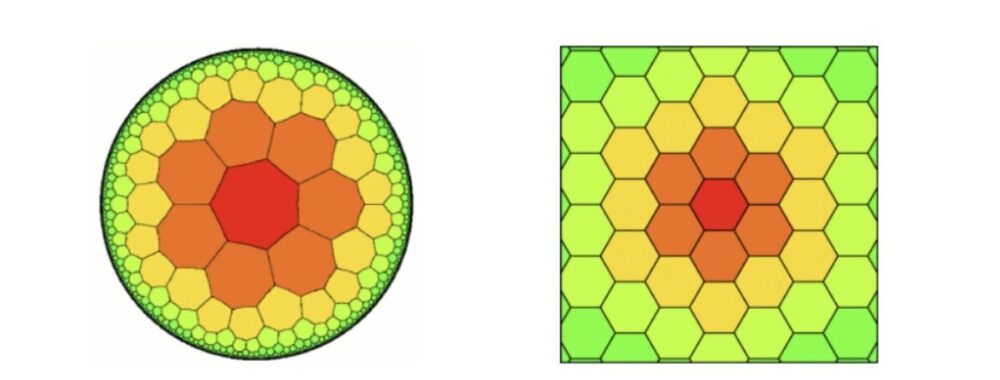

Hexagonal tessellations depicted in Euclidean rectangular geometry (right) and Poincaré disc model for hyperbolic geometry (left).

[1] Caroline Series andDavid Wright, Non-Euclidean geometry and Indra’s pearls,Plus Magazine, 2007 : http://plus.maths.org/content/non-euclidean-geometry-and-indras-pearls

Historically, it was believed that Euclidean geometry was the sole framework for describing the universe. However, advancements in math and science, particularly Einstein’s theory of relativity, revealed that space itself is curved and can be described using non-Euclidean geometry. As this revolutionary idea gained prominence, artists began incorporating these concepts into their work—sometimes intuitively, even if they didn’t fully grasp the underlying mathematics.

[2 ]Alexis Karpuzos, The Fourth Dimension in Art & Science:A visual narrative of the relationship between Science and Art, during the 20^th Century, Think Labs, Athens 2013 : http://www.slideshare.net/akarpuzos/the-4th-dimension-in-art-science

Non-Euclidean geometry revolutionized our understanding of space by introducing concepts like curvature and geodesics. In elliptic geometry, positive curvature bends space inward, as seen on the surface of a sphere. Conversely, hyperbolic geometry, with negative curvature, creates outwardly curved spaces resembling a saddle or pseudosphere. In these geometries, absolute straightness disappears; instead, “straight” paths are geodesics that curve along the surface. This fundamentally alters perceptions of space, distorting angles and perspectives while eliminating flat planes. These principles also underpin Einstein’s General Relativity, which describes the universe as a dynamic, curved spacetime.

 

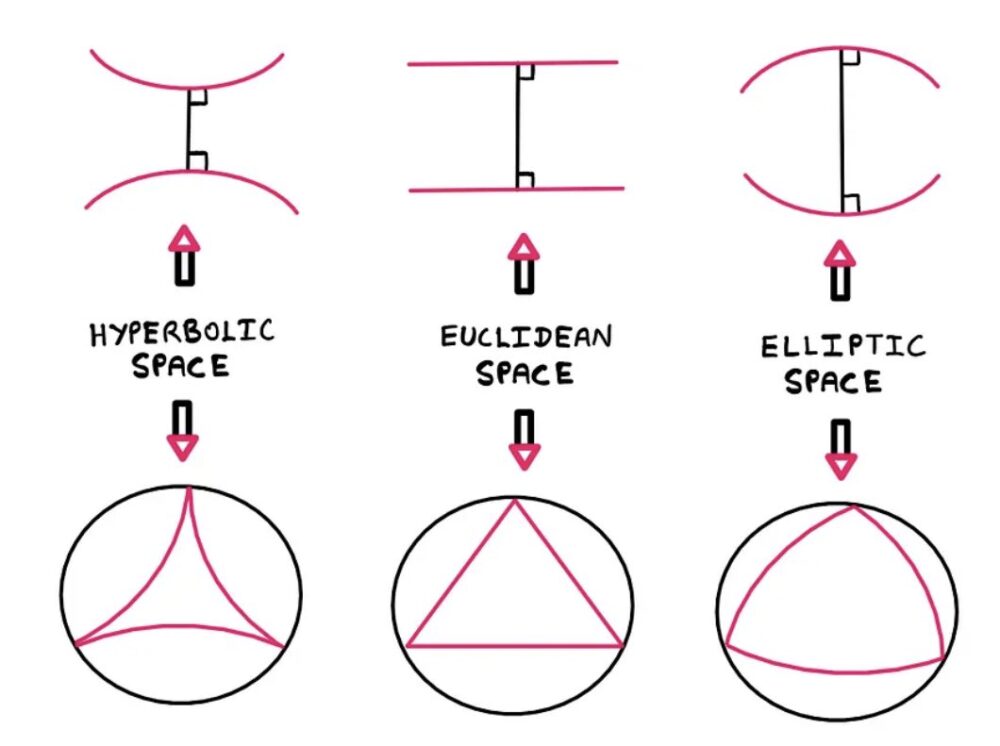
Image 3 depicts a simple perspective comparing the Euclidean Space with two Non-Euclidean spaces and difference in appearance of the same triangle graphed on each geometry.

[3] wikipedia, Non-Euclidean Geometry: History : http://en.wikipedia.org/wiki/Non-Euclidean_geometry(photo 3: simple geometric visual)

 

 

 

 

Artists have historically embraced these ideas to break traditional perspectives. M.C. Escher famously visualized hyperbolic geometry in works like his Circle Limit [4]  series and created impossible spaces in Relativity. Cubists and Futurists disrupted Euclidean norms by fracturing perspectives to show multiple viewpoints simultaneously.

 

 Salvador Dalí’s Corpus Hypercubus [5] incorporated a four-dimensional hypercube to symbolize transcendence, while Frank Stella used non-Euclidean curves to blur the boundaries between dimensions.

Circle limit [4] left, Corpus Hypercubus [5] right.

 

 

Surrealists like Yves Tanguy explored dreamlike, warped spaces that defied logical structure. Some, like Escher, collaborated directly with mathematicians, drawing inspiration from formal geometric principles.

[6] Reply to Red, Yves Tanguy

, contemporary artists can use non-Euclidean geometry to push creative boundaries further. Experimenting with perspective, hyperbolic tessellations, and immersive technology like virtual reality (VR) opens up endless possibilities. Tools such as generative algorithms and 3D modeling software enable the creation of intricate, curved spaces that feel infinite or otherworldly. By integrating science, art, and philosophy, modern works can symbolize themes like infinity, unity, or alternate realities. Non-Euclidean geometry remains a powerful tool for artists seeking to challenge perceptions and reimagine the visual language of space and form.

For an immersive experience through these geometries, I recommend this YouTube video:

[1] Caroline Series andDavid Wright, Non-Euclidean geometry and Indra’s pearls,Plus Magazine, 2007 : http://plus.maths.org/content/non-euclidean-geometry-and-indras-pearls

[2] Alexis Karpuzos, The Fourth Dimension in Art & Science:A visual narrative of the relationship between Science and Art, during the 20^th Century, Think Labs, Athens 2013 : http://www.slideshare.net/akarpuzos/the-4th-dimension-in-art-science

[3] Wikipedia, Non-Euclidean Geometry: History : http://en.wikipedia.org/wiki/Non-Euclidean_geometry

[4] Wikipedia , ” Circle Limit Exploration.” EscherMath: https://eschermath.org/wiki/Circle_Limit_Exploration.html.

[5] The Metropolitan Museum of Art. “Four-Dimensional Object (Hyper-Cube).” The Met Collection Online:  https://www.metmuseum.org/art/collection/search/488880.

[6] “Reply to Red, Yves Tanguy, 1943.” Artchive:  https://www.artchive.com/artwork/reply-to-red-yves-tanguy-1943/.

[7] YouTube. “Non-Euclidean Geometry Explored:https://youtu.be/yqUv2JO2BCs?si=VDfvznA89Tn4IHh_.

[8] OpenAI. (2025, January 20). ChatGPT [Language model]: https://chat.openai.com/